SEMANA 23

JULIO 13 AL 17






Mínimo común múltiplo(m.c.m.)

Estudiarás dos maneras de calcularlo:
1ª Por descomposición en sus factores primos.
2ª Por divisiones sucesivas.

 Calcular el m.c.m.(185,75)

Por el método de descomposición en sus factores primos, tenemos:

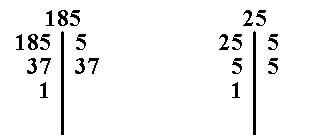
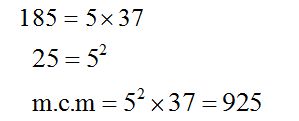
m.c.m.(185,25) = 925

Es tan sencillo el cálculo del m.c.m. que basta que sepas:

Se toman todos los factores que sean diferentes y los que sean iguales, el que tenga el exponente más grande. Si tienen iguales los exponentes, se toma uno de los factores.

En el último ejercicio vemos que tienen el factor 5 los dos números.

En este caso tomamos el de mayor exponente: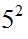 

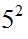
Factor diferente es el 37.

925 es el número más pequeño que podemos dividir entre 185 y 25 de modo que los cocientes son exactos. El resto vale cero.

3.73 Calcular el número más pequeño al que podemos dividir por 234 y 184, de modo que el resto sea cero:

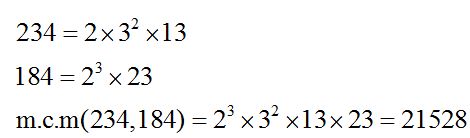
21528 es el número menor que al dividir por 234 y 184 obtenemos un cociente exacto, es decir, el resto vale cero.

3.74 Calcula el número más pequeño que existe que al dividir por 20631 y 3887 los cocientes sean exactos:

Respuesta: 268203

Por si has tenido dificultades:

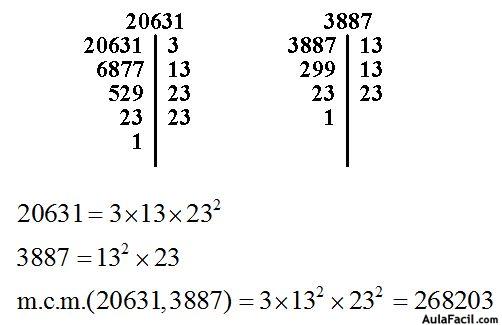
Hay un solo factor diferente que es el 3.
Los factores 13 y 23 que son comunes, tomamos con el mayor exponente.
268203 es el número más pequeño que existe de modo que al dividir por 20631 y 3887 los cocientes son exactos.

3.75 Calcula el m.c.m.(375,135)
Respuesta: 3375

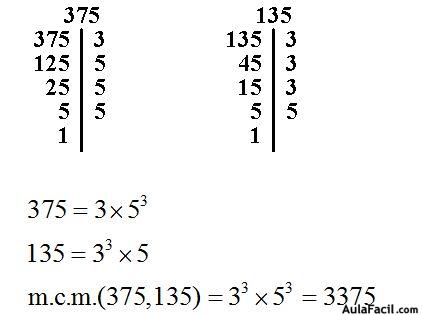
 Calcula el menor número existente que al dividirlo por 3059 y 1173 los cocientes son exactos:

Respuesta: 156009

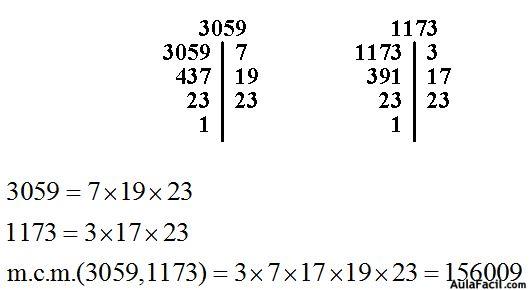
Máximo Común Divisor (M.C.D.)

El máximo común divisor (MCD) de dos o más número natural o enteros (no números con decimales) es el número más grande que les divide.

Para descubrir cuáles son los números que les divide existen dos formas: la forma larga y la forma corta. Esto lo explicaremos a través de un ejemplo. Ejemplo:

Forma larga

Máximo común divisor (MCD) de 10 y 20:

Divisor de 20: 1, 2, 4, 5, 10 y 20.

Divisor de 10: 1, 2, 5 y 10.

Importante: los divisores se sacan dividiendo, es decir, todo número que dividido por el número que estamos analizando de 0 en el resto. Por ejemplo:

10    5

0    2

10    6

4    1 

- 6 No sería divisor de 10 porque el resto da 4 y tiene que ser 0.

Una vez sabido que los divisores de 10 y de 20 son:

Divisor de 20: 1, 2, 4, 5, 10 y 20.

Divisor de 10: 1, 2, 5 y 10.

Vamos a ver cuáles son los números que coinciden que son:

Divisor de 20: 1, 2, 4, 5, 10 y 20.

Divisor de 10: 1, 2, 5 y 10.

Divisores de 10 y 20 son: 1, 2, 5 y 10.

El máximo común divisor sería el 10 porque es el número más grande que, a su vez, es divisor de ambos número (10 y 20).

Forma corta

Para número más grandes es más fácil hacer una descomposición en factores primos. Esta descomposición la empezamos siempre con el número más pequeño divisible del número que analizamos. Por ejemplo, para descubrir el máximo común divisor de 40 y 60. Escribimos el número que vamos a descomponer a la derecha (en este caso el 40) y seguidamente trazamos una recta vertical. Será detrás de esta donde colocaremos los factores primos empezando por el más pequeño. Haremos lo mismo con el 60.

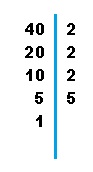En este paso hemos dividido 40:2=20. Ahora buscaremos el mínimo divisor de 20 que es 2 y hacemos lo mismo 20:2= 10. Y seguiremos haciendo lo mismo con todos los anteriores.

¡Truco! Si quieres saber si has hecho bien la descomposición de ffactores primos se puede comprobar multiplicando. Empezando por abajo, multiplicas el último número de la izquierda (multiplicando) con el último de la derecha (multiplicador), el resultado debe ser el número de arriba del multiplicando.

Ejemplo:

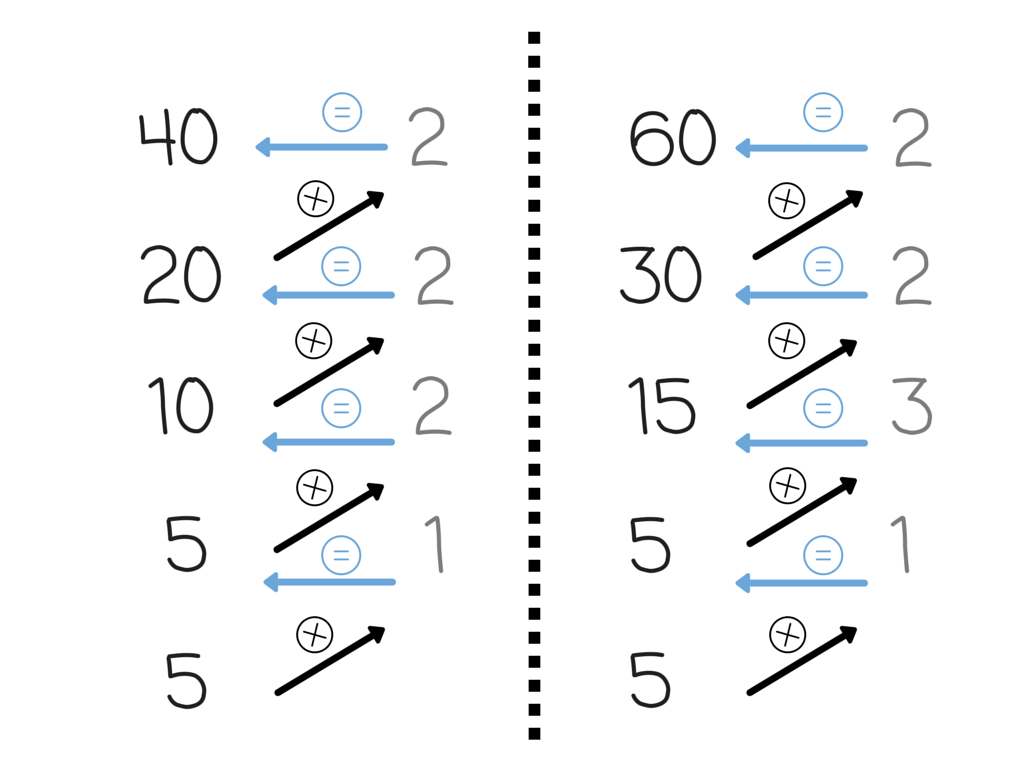El último número es el 5 (multiplicando) el multiplicador será el 1 y el resultado es el 5. Lo mismo pasa si 5 (multiplicando) lo multiplicas por 2 (multiplicador) es igual a 10.

Una vez descompuesto el número 40 sabemos que 40 es divisor de:

	MCD de 40 = 2x2x2x5

El mismo proceso seguiremos con el número 60:

Una vez fragmentados ambo

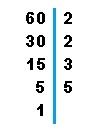MCD de 60 = 2x2x5x5

Una vez fragmentados ambos números vemos que:

Los divisores de 40 son: 2x2x2x5

Los divisores de 60 son: 2x2x3x5

Observamos cuales son los números que se repiten (los que estan en negrita) y los multiplicamos:

2x2x5= 20

El máximo común divisor de 40 y 60 es 20