OCTUBRE 19 AL 23
Talleres de repaso de operaciones con fraccionarios( suma, resta, multiplicación y división)----suma, resta, multiplicación de decimales, conversiones de medidas de longitud.
Matemáticas 6º
IE Jose Celestino Mutis. Profesora Emilse Garzón D.
lunes, 19 de octubre de 2015
domingo, 11 de octubre de 2015
SEMANA 36
OCTUBRE 12 A 16
LUNES 12----FESTIVO
Ángulos adyacentes, complementarios y suplementarios.
Multiplicación y división de fraccionarios.
Talleres.
LUNES 12----FESTIVO
Ángulos adyacentes, complementarios y suplementarios.
Multiplicación y división de fraccionarios.
Talleres.
domingo, 4 de octubre de 2015
SEMANA 35
OCTUBRE 5 AL 9
Taller nº 3 de geometría: medición de ángulos y clasificación de los mismos, medición de ángulos interiores de un triángulo.
Taller nº 3 de geometría: medición de ángulos y clasificación de los mismos, medición de ángulos interiores de un triángulo.
domingo, 27 de septiembre de 2015
SEMANA 34
SEPTIEMBRE 28 A OCTUBRE 2
TALLER
1. Realice la operación teniendo en cuenta el valor de la letra:
a= 1/2 b= 3/4 c= 4/3 d= 7/4
a) d-b
b) c-a
c) ( c+ d) - a
d) ( b+ d) -c
e) ( ( d-a) + b
f) a+ b+c
g) d - ( a+ b)
h) ( c+ d) - ( a+ b)
2. Multiplique ( simplifique si es posible):
a) 3/5 x 6/7
b) 6/11 x 11
c) 4 x 2/9
d) 1/3 x 3/8
e) 27/16 x 8/3
f) 7/5 x 5/2
g) 3/4 x 8
h) 2 1/4 x 6/13
domingo, 20 de septiembre de 2015
SEMANA 33
SEPTIEMBRE 21 AL 25
MULTIPLICACIÓN DE FRACCIONARIOS
Paso 3. Simplifica la fracción:
MULTIPLICACIÓN DE FRACCIONARIOS
Hay 3 simples pasos para multiplicar fracciones
1. Multiplica los números de arriba (los numeradores).
2. Multiplica los números de abajo (los denominadores).
3. Simplifica la fracción.
|
Ejemplo 1
| 1 | × | 2 |
| 2 | 5 |
Paso 1. Multiplica los números de arriba:
| 1 | × | 2 | = | 1 × 2 | = | 2 |
| 2 | 5 |
Paso 2. Multiplica los números de abajo:
| 1 | × | 2 | = | 1 × 2 | = | 2 |
| 2 | 5 | 2 × 5 | 10 |
| 2 | = | 1 |
| 10 | 5 |
(Si no estás seguro de cómo se hace el último paso ve a la página de Fracciones equivalentes)
Ejemplo 2
| 1 | × | 9 |
| 3 | 16 |
Paso 1. Multiplica los números de arriba:
| 1 | × | 9 | = | 1 × 9 | = | 9 |
| 3 | 16 |
Paso 2. Multiplica los números de abajo:
| 1 | × | 9 | = | 1 × 9 | = | 9 |
| 3 | 16 | 3 × 16 | 48 |
Paso 3. Simplifica la fracción:
| 9 | = | 3 |
| 48 | 16 |
miércoles, 16 de septiembre de 2015
domingo, 13 de septiembre de 2015
SEMANA 32
14 AL 18 DE SEPTIEMBRE
TALLER Nº 3
1. Realice las siguientes sumas de decimales:
a) 7,2+ 2810, 003+56, 32
b) 66,34+1,74+56,0004+25+132
c) 42+1,3+2,86+5+1,443+0,003
d) 26,8+56,46+34,5699+0,0073+16
e) 52+0,1+33,46+125,005+0,03
2. Restar y dar la prueba:
a) De 859 restar 72,66025
b) De 56,340003 restar 15,987362
c) De 172 restar 59,8412
e) De 456 restar 25,8413
5) De 958,32 restar 26,7565
3. Multiplicar:
a) 158,656 x 7,26
b) 125, 48 x 12,35
c) 725,48 x 2,36
d) 126,78 x 9,76
e) 100, 003 x 2,18
TALLER Nº 3
1. Realice las siguientes sumas de decimales:
a) 7,2+ 2810, 003+56, 32
b) 66,34+1,74+56,0004+25+132
c) 42+1,3+2,86+5+1,443+0,003
d) 26,8+56,46+34,5699+0,0073+16
e) 52+0,1+33,46+125,005+0,03
2. Restar y dar la prueba:
a) De 859 restar 72,66025
b) De 56,340003 restar 15,987362
c) De 172 restar 59,8412
e) De 456 restar 25,8413
5) De 958,32 restar 26,7565
3. Multiplicar:
a) 158,656 x 7,26
b) 125, 48 x 12,35
c) 725,48 x 2,36
d) 126,78 x 9,76
e) 100, 003 x 2,18
domingo, 6 de septiembre de 2015
SEMANA 31
Septiembre 7 al 11
TALLER Nº 1
Así que era lo mismo que 110 - 3 = 107, pero poniendo puntos decimales
TALLER Nº 1
Sumar decimales
Sumar decimales es fácil si lo haces ordenadamente
Para sumar decimales sigue estos pasos:
- Escribe los números, uno bajo el otro, con los puntos decimales alineados.
- Añade ceros para que los números tengan la misma longitud.
- Suma normalmente, y recuerda poner el punto decimal en la respuesta.
Ejemplo: suma 1,452 y 1,3
| Alinea los decimales: | 1,452 | ||
| + | 1,3 | ||
| "Rellena" con ceros: | 1,452 | ||
| + | 1,300 | ||
| Suma: | 1,452 | ||
| + | 1,300 | ||
| 2,752 |
Ejemplo: suma 3,25, 0,075 y 5
| Alinea los decimales: | 3,25 | ||
| 0,075 | |||
| + | 5. | ||
| "Rellena " con ceros: | 3,250 | ||
| 0,075 | |||
| + | 5,000 | ||
| Suma: | 3,250 | ||
| 0,075 | |||
| + | 5,000 | ||
| 8,325 |
Restar decimales
Restar decimales es fácil si lo haces ordenadamente
Para restar decimales sigue estos pasos:
- Escribe los dos números, uno bajo el otro, con los puntos decimales alineados.
- Añade ceros para que los números tengan la misma longitud.
- Suma normalmente, y recuerda poner el punto decimal en la respuesta.
Ejemplo: resta 0,03 de 1,1
| Alinea los decimales: | 1,1 | ||
| - | 0,03 | ||
| "Rellena" con ceros: | 1,10 | ||
| - | 0,03 | ||
| Resta: | 1,10 | ||
| - | 0,03 | ||
| 1,07 |
Así que era lo mismo que 110 - 3 = 107, pero poniendo puntos decimales
Ejemplo: calcula 7,005-0,55
| Alinea los decimales: | 7,005 | ||||||
| - | 0,55 | ||||||
| "Rellena" con ceros: | 7,005 | ||||||
| - | 0,550 | ||||||
| Resta: | 7,005 | ||||||
| - | 0,550 | ||||||
| 6,455
MULTIPLICACIÓN DE DECIMALES
Para multiplicar dos números decimales:
1 Se multiplican como si fueran números enteros.
2El resultado final es un número decimal cuyo número de decimales es igual a la suma del número de decimales de los dos factores.
Ejemplo:
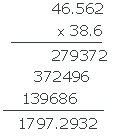
46,562 X 38,6 =
El primer factor tiene 3 decimales y el segundo 1, por tanto, el resultado tiene 4 decimales.
Multiplicación por la unidad seguida de ceros
Para multiplicar un número por la unidad seguida de ceros, se desplaza la coma hacia la derecha tantos lugares como ceros acompañen a la unidad.
Ejemplo:
|
domingo, 30 de agosto de 2015
SEMANA 30
AGOSTO 31 A SEPTIEMBRE 4
Talleres de repaso:
Suma, resta, multiplicación y división de racionales "Q"
Clases de triángulos según la medida de sus lados y de sus ángulos
Talleres de repaso:
Suma, resta, multiplicación y división de racionales "Q"
Clases de triángulos según la medida de sus lados y de sus ángulos
domingo, 23 de agosto de 2015
SEMANA 29
AGOSTO 24 AL 28
SE HARÁ EXAMEN DE FIN DE PERÍODO
Talleres realizados en el período tres:
Taller 1----
Realizar el taller de la fotocopia asignada en clase ( propiedad distributiva, ecuaciones, multiplicaciones abreviadas por 10, 100, 1000...propiedades de la potenciación.
Taller 2----
Aplique los criterios de divisibilidad por 2, 3, 4, 5, 6 9, 10 a cada uno de los siguientes números:
a) 1492
b) 640
c) 720
d) 1008
e) 31791
f) 40026
Taller 3----
1. Descomponer los siguientes números en factores primos:
a) 30
b) 900
c) 450
d)
245
e) 34
f) 39
g) 7986
h) 1024
i) 2187
2. Elabore un cuadro de 10 x 10 cm y construya la "criba de Erastótenes" y escriba los números d 1 a 100 ordenadamente.
a) Tache el 1 que no es primo( sólo tiene un divisor).
b) Tache los múltiplos de 2, pero no el 2.
c) Tache los múltiplos de 3, pero no el 3
d) Tache todos los múltiplos de 5, pero no el 5
e) Tache todos los múltiplos del 7, pero no el 7
f) Cuáles de los números de la criba, son simples y cuáles son compuestos? Explique.
Taller 4---
Calcule el m.c.m. de:
a) 15,120 y 200
b) 25, 50 y 75
c) 10, 100 y 1000
d) 9,18 y 36
e) 20, 25 y 30
f) 27, 81 y 18
Taller 5---
1. Halle el M. C. D. de:
a) 15, 18 y 27
b) 20, 25 y 30
c) 60 y 38
d) 100, 200 y 30
2. Escriba como se leen las siguientes fracciones ( de las tres formas vistas):
a) 1/3
b) 1/10
c) 5/10000
d) 7/5
e) 5/100
3. Escriba con n{umeros las siguientes expresiones:
a) Dos tercios
b) Cinco tercios
c) Un séptimo
d) Cinco sextos
e) Cuatro décimos
f) Tres quintos
4. Represente con gráficas y en la recta numérica, los siguientes números:
a) 2/8
b) 3/10
c) 6/9
d) 8/12
e) 4/7
Taller 6
b) 18 grados
c) 93 grados
d) 132 grados
e) 90 grados
2. Trace paralelas a las siguientes rectas y escriba como se lee:
TALLER 2---
Consultar:
1. Qué es un polígono?
2. Definir y graficar:
a) Triángulo
b) Cuadrilátero
c) Pentágono
d) Hexágono
e) Heptágono
f) Octágono
g) Eneágono
h) Decágono
TALLER 3---
Realizar las siguientes conversiones de medidas de longitud:
a) 7 Hectómetros a decímetros
b) 30 centímetros a metros
c) 80 metros a decímetros
d) 52 metros a centímetros
e) 25 decímetros a centímetros
f) 6 metros a centímetros
g) 8 kilómetros a milímetros
h) 986 Miriámtros a centímetros
i) 32,7 Decámetros a decímetros
j) 0,045 Kilómetros a centímetros
l) 456 centímetros a milímetros
m) 1825 decímetros a centímetros
TALLER 4---
Se realiza un estudio acerca del peso en Kilogramos de los estudiantes de un curso en la Institución educativa José Celestino Mutis, obteniendo los siguientes datos:
55,66,60,53,58,51,63,59,64,56,59,55,59,64,56,59,68,71,51,55,70,65,58,66,58,64,57,59,59,61,54,64,59,54,57,60,62,51.
a) Ordene los datos y encuentre número de datos.
b) Elabore la tabla de frecuencias y encuentre:
ÁNGULOS
Definición de ángulo
Se llama ángulo a la parte del plano delimitada por dos semirrectas que parten de un mismo punto llamado vértice. A cada semirrecta se le llama lado del ángulo.

- Los lados del ángulo son las semirrectas que lo forman.
- El vértice del ángulo es el punto común que es origen de los lados.
Los tipos de ángulos son:
Agudo < 90°
Recto = 90°
Obtuso > 90°
Convexo < 180°
Llano = 180°
Cóncavo > 180°
Completo = 360°
Nulo = 0º
Hoy hablaremos de los ángulos agudo, recto y obstuso.



2.3- Ángulos obtusos
Un ángulo obtuso es un ángulo que mide más de 90° pero menos de 180°.

3- Algunas cosas importantes que debes saber















SE HARÁ EXAMEN DE FIN DE PERÍODO
Talleres realizados en el período tres:
Taller 1----
Realizar el taller de la fotocopia asignada en clase ( propiedad distributiva, ecuaciones, multiplicaciones abreviadas por 10, 100, 1000...propiedades de la potenciación.
Taller 2----
Aplique los criterios de divisibilidad por 2, 3, 4, 5, 6 9, 10 a cada uno de los siguientes números:
a) 1492
b) 640
c) 720
d) 1008
e) 31791
f) 40026
Taller 3----
1. Descomponer los siguientes números en factores primos:
a) 30
b) 900
c) 450
d)
245
e) 34
f) 39
g) 7986
h) 1024
i) 2187
2. Elabore un cuadro de 10 x 10 cm y construya la "criba de Erastótenes" y escriba los números d 1 a 100 ordenadamente.
a) Tache el 1 que no es primo( sólo tiene un divisor).
b) Tache los múltiplos de 2, pero no el 2.
c) Tache los múltiplos de 3, pero no el 3
d) Tache todos los múltiplos de 5, pero no el 5
e) Tache todos los múltiplos del 7, pero no el 7
f) Cuáles de los números de la criba, son simples y cuáles son compuestos? Explique.
Taller 4---
Calcule el m.c.m. de:
a) 15,120 y 200
b) 25, 50 y 75
c) 10, 100 y 1000
d) 9,18 y 36
e) 20, 25 y 30
f) 27, 81 y 18
Taller 5---
1. Halle el M. C. D. de:
a) 15, 18 y 27
b) 20, 25 y 30
c) 60 y 38
d) 100, 200 y 30
2. Escriba como se leen las siguientes fracciones ( de las tres formas vistas):
a) 1/3
b) 1/10
c) 5/10000
d) 7/5
e) 5/100
3. Escriba con n{umeros las siguientes expresiones:
a) Dos tercios
b) Cinco tercios
c) Un séptimo
d) Cinco sextos
e) Cuatro décimos
f) Tres quintos
4. Represente con gráficas y en la recta numérica, los siguientes números:
a) 2/8
b) 3/10
c) 6/9
d) 8/12
e) 4/7
Taller 6
TALLERES DE GEOMETRÍA Y ESTADÍSTICA
TALLER 1----
1. medir con el transportador los siguientes ángulos. colocarles nombre, señalar sus lados y vértice.
a) 60 gradosb) 18 grados
c) 93 grados
d) 132 grados
e) 90 grados
2. Trace paralelas a las siguientes rectas y escriba como se lee:
TALLER 2---
Consultar:
1. Qué es un polígono?
2. Definir y graficar:
a) Triángulo
b) Cuadrilátero
c) Pentágono
d) Hexágono
e) Heptágono
f) Octágono
g) Eneágono
h) Decágono
TALLER 3---
Realizar las siguientes conversiones de medidas de longitud:
a) 7 Hectómetros a decímetros
b) 30 centímetros a metros
c) 80 metros a decímetros
d) 52 metros a centímetros
e) 25 decímetros a centímetros
f) 6 metros a centímetros
g) 8 kilómetros a milímetros
h) 986 Miriámtros a centímetros
i) 32,7 Decámetros a decímetros
j) 0,045 Kilómetros a centímetros
l) 456 centímetros a milímetros
m) 1825 decímetros a centímetros
TALLER 4---
Se realiza un estudio acerca del peso en Kilogramos de los estudiantes de un curso en la Institución educativa José Celestino Mutis, obteniendo los siguientes datos:
55,66,60,53,58,51,63,59,64,56,59,55,59,64,56,59,68,71,51,55,70,65,58,66,58,64,57,59,59,61,54,64,59,54,57,60,62,51.
a) Ordene los datos y encuentre número de datos.
b) Elabore la tabla de frecuencias y encuentre:
- Frecuencia absoluta(f)
- Frecuencia relativa(fr)
- Moda ( Mo)
- Mediana (Me)
- Media aritmética.
TALLER 5---
Observe los siguientes datos:
Edades: 2 a 4 años, 4 a 6 años, 6 a 8 años, 8 a 10 años, 10 a 12 años, 12 a 14 años.
Frecuencia :
f1= 34
f2=86
f3= 51
f4= 125
f6= 102
1) Elabore tabla de frecuencias teniendo en cuenta: edades, frecuencia absoluta y frecuencia relativa.
2) Realice diagrama de barras.
3) Elabore polígono de frecuencias.
4) Cuál es la moda( Mo) ?
TALLER 6---
Encontrar porcentajes:( haciendo los procedimientos completos)
a) El 12% de $25.000
b) El 25% de $80.000
c) El 72% de $150.000
d) El 13 % de $ 100.000
e) El 18% de 37 estudiantes.
TODOS LOS TALLERES DEBEN ESTAR DEBIDAMENTE SOLUCIONADOS CON PROCEDIMIENTOS, Y, LOS CUADERNOS SERÁN ENTREGADOS EL MISMO DÍA QUE SE REALICE EL EXÁMEN DE FINAL DE PERÍODO (QUE TIENE UN VALOR DE 30%)
TALLER 6---
Encontrar porcentajes:( haciendo los procedimientos completos)
a) El 12% de $25.000
b) El 25% de $80.000
c) El 72% de $150.000
d) El 13 % de $ 100.000
e) El 18% de 37 estudiantes.
TODOS LOS TALLERES DEBEN ESTAR DEBIDAMENTE SOLUCIONADOS CON PROCEDIMIENTOS, Y, LOS CUADERNOS SERÁN ENTREGADOS EL MISMO DÍA QUE SE REALICE EL EXÁMEN DE FINAL DE PERÍODO (QUE TIENE UN VALOR DE 30%)
TODOS LOS ESTUDIANTES DEBEN LLEVAR A CADA CLASE: REGLA, TRANSPORTADOR, COMPÁS, LÁPIZ Y BORRADOR. OBLIGATORIO COMO IMPLEMENTO DE ESTUDIO.
LOS ESTUDIANTES QUE AÚN NO HAN PRESENTADO EXÁMEN DE SUSTENTACIÓN DE REFUERZO DEL SEGUNDO PERÍODO, DEBEN HACERLO EN LA SEMANA 30 ( DEL 31 DE AGOSTO AL 30 DE SEPTIEMBRE), EN HORARIO DE CLASE.
LOS ESTUDIANTES QUE AÚN NO HAN PRESENTADO EXÁMEN DE SUSTENTACIÓN DE REFUERZO DEL SEGUNDO PERÍODO, DEBEN HACERLO EN LA SEMANA 30 ( DEL 31 DE AGOSTO AL 30 DE SEPTIEMBRE), EN HORARIO DE CLASE.
ÁNGULOS
1- Ángulos
Se toma un punto del plano y partiendo de ese punto, se dibujan dos semirrectas. A la abertura formada por las dos semirrectas se le llama ángulo.
Definición de ángulo
Se llama ángulo a la parte del plano delimitada por dos semirrectas que parten de un mismo punto llamado vértice. A cada semirrecta se le llama lado del ángulo.

- Los lados del ángulo son las semirrectas que lo forman.
- El vértice del ángulo es el punto común que es origen de los lados.
Los tipos de ángulos son:
Agudo < 90°
Recto = 90°
Obtuso > 90°
Convexo < 180°
Llano = 180°
Cóncavo > 180°
Completo = 360°
Nulo = 0º
Hoy hablaremos de los ángulos agudo, recto y obstuso.
2- Tipos de ángulos según su medida
| Agudo < 90° | Recto = 90° | Obtuso>90° |

2.1- Ángulos rectos
Un ángulo recto es un ángulo que mide exactamente 90°. Si te das cuenta, en la esquina del ángulo hay unsímbolo especial, una caja. Si ves ese símbolo, el ángulo es recto. No se suele escribir el 90°. Si ves la cajaen la esquina ya te están diciendo que es un ángulo recto.
Un ángulo recto es un ángulo que mide exactamente 90°. Si te das cuenta, en la esquina del ángulo hay unsímbolo especial, una caja. Si ves ese símbolo, el ángulo es recto. No se suele escribir el 90°. Si ves la cajaen la esquina ya te están diciendo que es un ángulo recto.

Un ángulo recto puede estar en cualquier orientación o giro, lo que importa es que el ángulo interior sea 90°
2.2- Ángulos agudos
Un ángulo agudo es un ángulo que mide menos de 90°.
Un ángulo agudo es un ángulo que mide menos de 90°.

Acuérdate de fijarte en cuál de los dos ángulos es al que se refiere uno. Si el ángulo pequeño es menor que90° entonces ese es agudo.
2.3- Ángulos obtusos
Un ángulo obtuso es un ángulo que mide más de 90° pero menos de 180°.

Acuérdate de fijarte en cuál de las dos partes es a la que se refiere uno. El ángulo más pequeño entre laslíneas es obtuso si mide entre 90° y 180°.
3- Algunas cosas importantes que debes saber
-Los ángulos que miden 180° se denominan ángulos extendidos o llanos.

- Los ángulos que miden más de 180° y menos de 360° se denominan ángulos cóncavos.

- Los ángulos que miden 360° se denominan ángulos completos.

- El ángulo nulo está formado por dos semirrectas coincidentes, por lo que su abertura es nula, es decir, 0°.

- Los ángulos pueden nombrarse utilizando letras griegas. Por ejemplo:


4- Cómo medir ángulos usando el transportador
Medir un ángulo significa determinar su amplitud y, para hacerlo generalmente se utiliza el transportador.
Un transportador es un instrumento en forma circular o semicircular y graduado angularmente.

Los ángulos se miden en grados sexagesimales. Un grado corresponde a la medida del ángulo que se forma cuando una circunferencia se divide en 360 partes iguales.
Los grados indican la separación de los lados del ángulo. Mientras más separados están los rayos que forman el ángulo, mayor esla cantidad de grados que este mide.
4.1- Para medir ángulos utilizando el transportador semicircular debes:
1° Colocar el trazo recto del transportador sobre uno de los lados del ángulo.
1° Colocar el trazo recto del transportador sobre uno de los lados del ángulo.
2° Hcer que el punto medio de ese trazo coincida con el vértice del ángulo.
3° Observar el otro lado del ángulo y su valor según la escala angular del transportador. Si el ángulo está abierto hacia la izquierdadebes fijarte en la escala externa y si está abierto hacia la derecha en la escala interna.
4.2- Para medir ángulos utilizando el transportador circular debes:
1° Colocar uno de los lados del ángulo frente al 0°.
1° Colocar uno de los lados del ángulo frente al 0°.
2° Hacer coincidir el centro de la circunferencia con el vértice del ángulo.
3° Observar el otro lado del ángulo y su valor según la escala angular del transportador.
Tipos de ángulos según su posición
Ángulos consecutivos
Ángulos consecutivos son aquellos que tienen el vértice y un lado común.

Ángulos adyacentes
Ángulos adyacentes son aquellos que tienen el vértice y un lado común, y los otros lados situados uno en prolongación del otro. Forman un ángulo llano.

Ángulos opuestos por el vértice:
Son los que teniendo el vértice común, los lados de uno son prolongación de los lados del otro.

Los ángulos 1 y 3 son iguales.
Los ángulos 2 y 4 son iguales.
Clases de ángulos según su suma
Ángulos complementarios:
Dos ángulos son complementarios si suman 90°.

Ángulos suplementarios
Dos ángulos son suplementarios si suman 180°.

Ángulos entre paralelas y una recta transversal
Ángulos correspondientes
Los ángulos 1 y 2 son iguales.

. Ángulos alternos internos
Los ángulos 2 y 3 son iguales.

Ángulos alternos externos
Los ángulos 1 y 4 son iguales.

lunes, 17 de agosto de 2015
SEMANA 28
AGOSTO 17 AL 21
TALLER N° 1
TEMA: ORGANIZACIÓN DE DATOS ESTADÍSTICOS
1- Ordene de menor a mayor las calificaciones obtenidas por un grupo de estudiantes, en un examen, y luego organícelas en una tabla de datos.
65, 87, 76, 54, 92,74, 65, 51, 43, 98,45, 36, 95, 50, 88,69, 71, 82, 100, 100.
a- A qué clase de variable corresponde la información recogida?
2- En la clase de Educación Física, el profesor toma los datos de 40 alumnos sobre la estatura de cada uno de los estudiantes, ordene los datos de menor a mayor y organícelos en una tabla de datos.
1.50 -1.58 -1.60 -1.52 -1.58 -1.48 -1.65 -1.70 -1.62 -1.65 -1.63 -1.58 -1.51 -1.59 1.49 -1.53 -1.57 -1.73 -1.76 -1.70 -1.49- 1.70 -1.58- 1.51 -1.68 -1.62 -1.53 -1.73 1.59 -1.50 -1.66 -1.47 -1.63 -1.58 -1.54 -1.71 -1.79 -1.56 -1.64 -1.57
a- A qué clase de variable corresponde la información recogida?
3- Realice y diseñe una encuesta a 25 personas sobre la clase de música (romántica, clásica,rock, pop, metálica, jazz, reggae,bachata, rancheras,salsa, vallenato, etc.), grupo musical (Kizz, Aerosmith, Los Inquietos, Binomio de Oro, etc.) cantante (don Omar, Daddy Yankee, Armik, Vanessa Mae, Diomedes Díaz, Enrique Iglesias, etc) de su preferencia, organice la información en una tabla de datos.
Determine el tipo de variable a que corresponde cada característica encuestada.
4- Diseñe una encuesta sobre deportes, equipos y deportistas de su preferencia y con sus compañeros de clase o colegio recoja la información, organícela en una tabla de datos. (mínimo 30 encuestados).
Determine el tipo de variable a que corresponde cada característica encuestada.
TALLER N° 2
TEMA: FRECUENCIAS
1- Se quiere saber el número de hijos por matrimonio del barrio Villa hermosa en Medellín. Para ello, se elige una muestra representativa de 50 matrimonios de ella.
Se obtienen los siguientes datos:
2 , 3 , 4 , 1 , 5 , 5 , 3 , 2 , 1 , 0 , 3 , 4 , 1 , 6 , 0 , 5 , 3 , 2 , 7 , 4 , 2 , 4 , 0 , 5 , 1 , 4 , 2 , 2 , 4 , 1 , 3 , 2 , 1 , 2 , 4 , 6 , 3 , 3 , 2 , 2 , 1 , 2 , 4 , 1 , 0 , 3 , 2 , 3 , 3 , 1 .
El número total de datos se representa con la letra n.
En este ejemplo n = 50 .
A- Organice la información en una tabla de datos.
B- Realice las tablas de las diferentes frecuencias.
C- Halle la frecuencia absoluta (f)
D- Halle la frecuencia relativa (fr)
E- Halle la frecuencia absoluta acumulada (F)
F- Halle la frecuencia relativa acumulada (Fr)
G- Halle la frecuencia porcentual (fi%)
H- Halle la frecuencia acumulada porcentual (Fi%)
2- Un científico cree que el color rojo tiene un mayor grado de para las palomas, que el verde. Para comprobar su hipótesis expuso a 15 palomas a una sesión completa de condicionamiento operante que consistía en poner a las palomas en una caja que tenía dos luces (una roja y una verde) y un comedero. Las palomas debían picotear cualquiera de las luces para recibir comida.
Algunas veces picoteaban la luz roja y otras, la verde.
Cada sesión duraba 30 minutos y las respuestas que dieron las palomas durante ese transcurso de tiempo fueron las siguientes:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Rojo 76 49 66 82 57 67 72 84 63 59 56 64 68 81 79
Verde 63 53 65 91 85 12 53 62 56 42 40 32 50 60 23
A-Identifique la población de estudio y la muestra que representa a dicha población.
B- ¿Cuál es la variable que se está midiendo? ¿De qué tipo es?
C- Halle y haga las tablas de frecuencias absoluta, relativa, absoluta acumulada, relativa acumulada, porcentual, porcentual acumulada que representen la situación.
3- Manuela preguntó a sus compañeros de curso por la fruta que preferían comer a la hora del descanso. Los datos que recogió fueron los siguientes: manzana, pera, mango, mango, banano, pera, manzana, manzana, manzana, pera, manzana, mango, banano, mango, manzana, manzana, pera, mango, banano, mango, manzana, pera, mango, mango, manzana, manzana, manzana, banano, pera, pera, manzana, manzana, banano, banano, pera, pera, manzana, banano, manzana, pera.
A- Realice la tabla de datos
B- Halle y haga las tablas de frecuencias.
C- Contestar las siguientes preguntas:
a. ¿Cuántos alumnos prefieren mango?
b. ¿Cuál es la fruta que más prefieren?
c. ¿Cuál es la fruta que menos prefieren?
d. ¿A cuántos niños encuestó Manuela?
4- En un salón de belleza se lleva el registro de las tinturas aplicadas a sus clientas. El siguiente es el registro del día anterior: negro, rubio, castaño, negro, negro, negro, negro, rubio, rubio, castaño, castaño, negro, negro, negro, negro, negro, negro, castaño, rubio, rubio, rubio, castaño, negro, negro, negro, negro, rubio, negro, negro, castaño.
A- Realice la respectiva tabla de datos
B- Halle y realice las frecuencias y sus respectivas tablas
C- Responda las preguntas
a. ¿A cuántas personas se les aplicó tinte de color rubio?
b. ¿Cuál es la frecuencia relativa de las personas a quienes se les aplicó tinte castaño?
c. ¿A qué porcentaje de personas se les aplicó tinte negro?
d. ¿Cuál es el color de tinte que menos se aplicó? ¿
A qué porcentaje equivale?
5- Los resultados de un test de inteligencia que midió el cociente intelectual de 25 personas, fueron los siguientes:
121, 100, 92, 100, 75, 75, 121, 92, 75, 92, 100, 121, 150, 97, 92, 75, 121, 150, 150, 100, 97, 92, 97, 121, 100.
A- Organizar la información en una tabla de datos
B- Hallar las frecuencias y elaborar su respectiva tabla de frecuencias.
C- Responda las preguntas:
a- ¿Cuántas personas tienen un coeficiente intelectual por debajo de 100?
b- Si se consideran personas superdotadas aquellas que tienen un coeficiente intelectual superior a 130, ¿cuántas personas superdotadas hay en el grupo? ¿A qué porcentaje equivalen?
c-¿Qué porcentaje de personas tiene coeficiente intelectual mayor o igual 100?
d-¿Cuál es la frecuencia relativa de las personas con coeficiente intelectual 75?
TALLER N° 3
TEMA: MEDIDAS DE TENDENCIA CENTRAL
1- Los siguientes datos corresponden a los ríos más caudalosos del país.
18-----FESTIVO
TALLER N° 1
TEMA: ORGANIZACIÓN DE DATOS ESTADÍSTICOS
1- Ordene de menor a mayor las calificaciones obtenidas por un grupo de estudiantes, en un examen, y luego organícelas en una tabla de datos.
65, 87, 76, 54, 92,74, 65, 51, 43, 98,45, 36, 95, 50, 88,69, 71, 82, 100, 100.
a- A qué clase de variable corresponde la información recogida?
2- En la clase de Educación Física, el profesor toma los datos de 40 alumnos sobre la estatura de cada uno de los estudiantes, ordene los datos de menor a mayor y organícelos en una tabla de datos.
1.50 -1.58 -1.60 -1.52 -1.58 -1.48 -1.65 -1.70 -1.62 -1.65 -1.63 -1.58 -1.51 -1.59 1.49 -1.53 -1.57 -1.73 -1.76 -1.70 -1.49- 1.70 -1.58- 1.51 -1.68 -1.62 -1.53 -1.73 1.59 -1.50 -1.66 -1.47 -1.63 -1.58 -1.54 -1.71 -1.79 -1.56 -1.64 -1.57
a- A qué clase de variable corresponde la información recogida?
3- Realice y diseñe una encuesta a 25 personas sobre la clase de música (romántica, clásica,rock, pop, metálica, jazz, reggae,bachata, rancheras,salsa, vallenato, etc.), grupo musical (Kizz, Aerosmith, Los Inquietos, Binomio de Oro, etc.) cantante (don Omar, Daddy Yankee, Armik, Vanessa Mae, Diomedes Díaz, Enrique Iglesias, etc) de su preferencia, organice la información en una tabla de datos.
Determine el tipo de variable a que corresponde cada característica encuestada.
4- Diseñe una encuesta sobre deportes, equipos y deportistas de su preferencia y con sus compañeros de clase o colegio recoja la información, organícela en una tabla de datos. (mínimo 30 encuestados).
Determine el tipo de variable a que corresponde cada característica encuestada.
TALLER N° 2
TEMA: FRECUENCIAS
1- Se quiere saber el número de hijos por matrimonio del barrio Villa hermosa en Medellín. Para ello, se elige una muestra representativa de 50 matrimonios de ella.
Se obtienen los siguientes datos:
2 , 3 , 4 , 1 , 5 , 5 , 3 , 2 , 1 , 0 , 3 , 4 , 1 , 6 , 0 , 5 , 3 , 2 , 7 , 4 , 2 , 4 , 0 , 5 , 1 , 4 , 2 , 2 , 4 , 1 , 3 , 2 , 1 , 2 , 4 , 6 , 3 , 3 , 2 , 2 , 1 , 2 , 4 , 1 , 0 , 3 , 2 , 3 , 3 , 1 .
El número total de datos se representa con la letra n.
En este ejemplo n = 50 .
A- Organice la información en una tabla de datos.
B- Realice las tablas de las diferentes frecuencias.
C- Halle la frecuencia absoluta (f)
D- Halle la frecuencia relativa (fr)
E- Halle la frecuencia absoluta acumulada (F)
F- Halle la frecuencia relativa acumulada (Fr)
G- Halle la frecuencia porcentual (fi%)
H- Halle la frecuencia acumulada porcentual (Fi%)
2- Un científico cree que el color rojo tiene un mayor grado de para las palomas, que el verde. Para comprobar su hipótesis expuso a 15 palomas a una sesión completa de condicionamiento operante que consistía en poner a las palomas en una caja que tenía dos luces (una roja y una verde) y un comedero. Las palomas debían picotear cualquiera de las luces para recibir comida.
Algunas veces picoteaban la luz roja y otras, la verde.
Cada sesión duraba 30 minutos y las respuestas que dieron las palomas durante ese transcurso de tiempo fueron las siguientes:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Rojo 76 49 66 82 57 67 72 84 63 59 56 64 68 81 79
Verde 63 53 65 91 85 12 53 62 56 42 40 32 50 60 23
A-Identifique la población de estudio y la muestra que representa a dicha población.
B- ¿Cuál es la variable que se está midiendo? ¿De qué tipo es?
C- Halle y haga las tablas de frecuencias absoluta, relativa, absoluta acumulada, relativa acumulada, porcentual, porcentual acumulada que representen la situación.
3- Manuela preguntó a sus compañeros de curso por la fruta que preferían comer a la hora del descanso. Los datos que recogió fueron los siguientes: manzana, pera, mango, mango, banano, pera, manzana, manzana, manzana, pera, manzana, mango, banano, mango, manzana, manzana, pera, mango, banano, mango, manzana, pera, mango, mango, manzana, manzana, manzana, banano, pera, pera, manzana, manzana, banano, banano, pera, pera, manzana, banano, manzana, pera.
A- Realice la tabla de datos
B- Halle y haga las tablas de frecuencias.
C- Contestar las siguientes preguntas:
a. ¿Cuántos alumnos prefieren mango?
b. ¿Cuál es la fruta que más prefieren?
c. ¿Cuál es la fruta que menos prefieren?
d. ¿A cuántos niños encuestó Manuela?
4- En un salón de belleza se lleva el registro de las tinturas aplicadas a sus clientas. El siguiente es el registro del día anterior: negro, rubio, castaño, negro, negro, negro, negro, rubio, rubio, castaño, castaño, negro, negro, negro, negro, negro, negro, castaño, rubio, rubio, rubio, castaño, negro, negro, negro, negro, rubio, negro, negro, castaño.
A- Realice la respectiva tabla de datos
B- Halle y realice las frecuencias y sus respectivas tablas
C- Responda las preguntas
a. ¿A cuántas personas se les aplicó tinte de color rubio?
b. ¿Cuál es la frecuencia relativa de las personas a quienes se les aplicó tinte castaño?
c. ¿A qué porcentaje de personas se les aplicó tinte negro?
d. ¿Cuál es el color de tinte que menos se aplicó? ¿
A qué porcentaje equivale?
5- Los resultados de un test de inteligencia que midió el cociente intelectual de 25 personas, fueron los siguientes:
121, 100, 92, 100, 75, 75, 121, 92, 75, 92, 100, 121, 150, 97, 92, 75, 121, 150, 150, 100, 97, 92, 97, 121, 100.
A- Organizar la información en una tabla de datos
B- Hallar las frecuencias y elaborar su respectiva tabla de frecuencias.
C- Responda las preguntas:
a- ¿Cuántas personas tienen un coeficiente intelectual por debajo de 100?
b- Si se consideran personas superdotadas aquellas que tienen un coeficiente intelectual superior a 130, ¿cuántas personas superdotadas hay en el grupo? ¿A qué porcentaje equivalen?
c-¿Qué porcentaje de personas tiene coeficiente intelectual mayor o igual 100?
d-¿Cuál es la frecuencia relativa de las personas con coeficiente intelectual 75?
TALLER N° 3
TEMA: MEDIDAS DE TENDENCIA CENTRAL
1- Los siguientes datos corresponden a los ríos más caudalosos del país.
A- Organice la tabla con los datos de cada variable de menor a mayor
B- ¿Cuál es el rango de las longitudes, las cuencas y los caudales de estos ríos? C- Determine la moda, la mediana y la media aritmética para cada variable.
D- ¿Cuáles de estos ríos tienen una longitud mayor que la longitud correspondiente a la mediana?
E- ¿Cuáles de estos ríos tienen una cuenca hidrográfica cuyo valor esté por debajo de la mediana?
F- ¿El valor de la mediana para la cuenca, la longitud y el caudal de estos ríos corresponde al mismo río?¿Cuál (o cuáles) es (son) ese (esos) río(s)?
2- Las puntuaciones obtenidas por un grupo de en una prueba han sido:
15, 20, 15, 18, 22, 13, 13, 16, 15, 19, 18, 15, 16, 20, 16, 15, 18, 16, 14, 13.
A- Ordene los datos de menor a mayor.
B- Determine el rango
C- Halle la moda, mediana y la media aritmética.
3, 3, 4, 3, 4, 3, 1, 3, 4, 3, 3, 3, 2, 1, 3, 3, 3, 2, 3, 2, 2, 3, 3, 3, 2, 2, 2, 2, 2, 3, 2, 1, 1, 1, 2, 2, 4, 1.
3-El número de estrellas de los hoteles de una ciudad viene dado por la siguiente serie:
A- Ordene los datos de menor a mayor.
B- Determine el rango.
C- Halle la moda , la mediana y la media aritmética.
4- Las calificaciones de 50 alumnos en Matemáticas han sido las siguientes:
5, 2, 4, 9, 7, 4, 5, 6, 5, 7, 7, 5, 5, 2, 10, 5, 6, 5, 4, 5, 8, 8, 4, 0, 8, 4, 8, 6, 6, 3, 6, 7, 6, 6, 7, 6, 7, 3, 5, 6, 9, 6, 1, 4, 6, 3, 5, 5, 6, 7.
A- Ordene los datos de menor a mayor.
B- Determine el rango.
C- Halle la moda, la mediana y la media aritmética.
5- Calcular el rango, la media, la mediana y la moda de la siguiente serie de números:
5, 3, 6, 5, 4, 5, 2, 8, 6, 5, 4, 8, 3, 4, 5, 4, 8, 2, 5, 4.
6- Calcular la media, la mediana y la moda y el rango de la siguiente serie de números:
5, 3, 6, 5, 4, 5, 2, 8, 6, 5, 4, 8, 3, 4, 5, 4, 8, 2, 5, 4.
domingo, 9 de agosto de 2015
lunes, 3 de agosto de 2015
SEMANA 26
AGOSTO 3 AL 7
MEDIDAS DE TENDENCIA CENTRAL
Son: Media aritmética, mediana y moda.
La media aritmética es el valor obtenido por la suma de todos sus valores dividida entre el número de sumadores.
Por ejemplo, las notas de 5 alumnos en una prueba:
La media aritmética es, probablemente, uno de los parámetros estadísticos más extendidos. Se le llama también promedio o, simplemente, media.
La moda:
La moda es el dato más repetido de la encuesta, el valor de la variable con mayor frecuencia absoluta.
Por ejemplo, el número de personas en distintos vehículos en una carretera: 5-7-4-6-9-5-6-1-5-3-7.
El número que más se repite es 5, entonces la moda es 5.
MEDIDAS DE TENDENCIA CENTRAL
Son: Media aritmética, mediana y moda.
La media aritmética es el valor obtenido por la suma de todos sus valores dividida entre el número de sumadores.
Por ejemplo, las notas de 5 alumnos en una prueba:
niño nota
1 6,0 ·Primero, se suman las notas: 2 5,4 6,0+5,4+3,1+7,0+6,1 = 27,6 3 3,1 ·Luego el total se divide entre la cantidad de alumnos: 4 7,0 27,6/5=5,52 5 6,1· La media aritmética en este ejemplo es 5,52
La media aritmética es, probablemente, uno de los parámetros estadísticos más extendidos. Se le llama también promedio o, simplemente, media.
La moda:
La moda es el dato más repetido de la encuesta, el valor de la variable con mayor frecuencia absoluta.
Por ejemplo, el número de personas en distintos vehículos en una carretera: 5-7-4-6-9-5-6-1-5-3-7.
El número que más se repite es 5, entonces la moda es 5.
Mediana:
La mediana es un valor de la variable que deja por debajo de sí a la mitad de los datos, una vez que éstos están ordenados de menor a mayor.
Por ejemplo, la mediana del número de hijos de un conjunto de trece familias, cuyos respectivos hijos son:
3, 4, 2, 3, 2, 1, 1, 2, 1, 1, 2, 1 y 1, es 2, puesto que, una vez ordenados los datos: 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 4, el que ocupa la posición central es 2.
domingo, 26 de julio de 2015
SEMANA 25
JULIO 27 AL 31
HISTORIA DE LA ESTADÍSTICA
Actividad:Los comienzos de la estadística pueden ser hallados en el antiguo Egipto, cuyos faraones lograron recopilar, hacia el año 3050 antes de Cristo, prolijos datos relativos a la población y la riqueza del país. De acuerdo al historiador griego Heródoto, dicho registro de riqueza y población se hizo con el objetivo de preparar la construcción de las pirámides. En el mismo Egipto, Ramsés II hizo un censo de las tierras con el objeto de verificar un nuevo reparto.En el antiguo Israel la Biblia da referencias, en el libro de los Números, de los datos estadísticos obtenidos en dos recuentos de la población hebrea. El rey David por otra parte, ordenó a Joab, general del ejército hacer un censo de Israel con la finalidad de conocer el número de la población.También los chinos efectuaron censos hace más de cuarenta siglos. Los griegos efectuaron censos periódicamente con fines tributarios, sociales (división de tierras) y militares (cálculo de recursos y hombres disponibles). La investigación histórica revela que se realizaron 69 censos para calcular los impuestos, determinar los derechos de voto y ponderar la potencia guerrera.Pero fueron los romanos, maestros de la organización política, quienes mejor supieron emplear los recursos de la estadística. Cada cinco años realizaban un censo de la población y sus funcionarios públicos tenían la obligación de anotar nacimientos, defunciones y matrimonios, sin olvidar los recuentos periódicos del ganado y de las riquezas contenidas en las tierras conquistadas. Para el nacimiento de Cristo sucedía uno de estos empadronamientos de la población bajo la autoridad del imperio.Durante los mil años siguientes a la caída del imperio Romano se realizaron muy pocas operaciones Estadísticas, con la notable excepción de las relaciones de tierras pertenecientes a la Iglesia, compiladas por Pipino el Breve en el 758 y por Carlomagno en el 762 DC. Durante el siglo IX se realizaron en Francia algunos censos parciales de siervos. En Inglaterra, Guillermo el Conquistador recopiló el Domesday Book o libro del Gran Catastro para el año 1086, un documento de la propiedad, extensión y valor de las tierras de Inglaterra. Esa obra fue el primer compendio estadístico de Inglaterra.Aunque Carlomagno, en Francia; y Guillermo el Conquistador, en Inglaterra, trataron de revivir la técnica romana, los métodos estadísticos permanecieron casi olvidados durante la Edad Media.Durante los siglos XV, XVI, y XVII, hombres como Leonardo de Vinci, Nicolás Copérnico, Galileo, Neper, William Harvey, Sir Francis Bacon y René Descartes, hicieron grandes operaciones al método científico, de tal forma que cuando se crearon los Estados Nacionales y surgió como fuerza el comercio internacional existía ya un método capaz de aplicarse a los datos económicos.Para el año 1532 empezaron a registrarse en Inglaterra las defunciones debido al temor que Enrique VII tenía por la peste. Más o menos por la misma época, en Francia la ley exigió a los clérigos registrar los bautismos, fallecimientos y matrimonios. Durante un brote de peste que apareció a fines de la década de 1500, el gobierno inglés comenzó a publicar estadísticas semanales de los decesos. Esa costumbre continuó muchos años, y en 1632 estos Bills of Mortality (Cuentas de Mortalidad) contenían los nacimientos y fallecimientos por sexo. En 1662, el capitán John Graunt usó documentos que abarcaban treinta años y efectuó predicciones sobre el número de personas que morirían de varias enfermedades y sobre las proporciones de nacimientos de varones y mujeres que cabría esperar. El trabajo de Graunt, condensado en su obra Natural and Political Observations...Made upon the Bills of Mortality (Observaciones Políticas y Naturales ... Hechas a partir de las Cuentas de Mortalidad), fue un esfuerzo innovador en el análisis estadístico.Por el año 1540 el alemán Sebastián Muster realizó una compilación estadística de los recursos nacionales, comprensiva de datos sobre organización política, instrucciones sociales, comercio y poderío militar. Durante el siglo XVII aportó indicaciones más concretas de métodos de observación y análisis cuantitativo y amplió los campos de la inferencia y la teoría Estadística.Los eruditos del siglo XVII demostraron especial interés por la Estadística Demográfica como resultado de la especulación sobre si la población aumentaba, decrecía o permanecía estática.En los tiempos modernos tales métodos fueron resucitados por algunos reyes que necesitaban conocer las riquezas monetarias y el potencial humano de sus respectivos países. El primer empleo de los datos estadísticos para fines ajenos a la política tuvo lugar en 1691 y estuvo a cargo de Gaspar Neumann, un profesor alemán que vivía en Breslau. Este investigador se propuso destruir la antigua creencia popular de que en los años terminados en siete moría más gente que en los restantes, y para lograrlo hurgó pacientemente en los archivos parroquiales de la ciudad. Después de revisar miles de partidas de defunción pudo demostrar que en tales años no fallecían más personas que en los demás. Los procedimientos de Neumann fueron conocidos por el astrónomo inglés Halley, descubridor del cometa que lleva su nombre, quien los aplicó al estudio de la vida humana. Sus cálculos sirvieron de base para las tablas de mortalidad que hoy utilizan todas las compañías de seguros.Durante el siglo XVII y principios del XVIII, matemáticos como Bernoulli, Francis Maseres, Lagrange y Laplace desarrollaron la teoría de probabilidades. No obstante durante cierto tiempo, la teoría de las probabilidades limitó su aplicación a los juegos de azar y hasta el siglo XVIII no comenzó a aplicarse a los grandes problemas científicos.Godofredo Achenwall, profesor de la Universidad de Gotinga, acuñó en 1760 la palabra estadística, que extrajo del término italiano statista (estadista). Creía, y con sobrada razón, que los datos de la nueva ciencia serían el aliado más eficaz del gobernante consciente. La raíz remota de la palabra se halla, por otra parte, en el término latino status, que significa estado o situación; Esta etimología aumenta el valor intrínseco de la palabra, por cuanto la estadística revela el sentido cuantitativo de las más variadas situaciones.Jacques Quételect es quien aplica las Estadísticas a las ciencias sociales. Este interpretó la teoría de la probabilidad para su uso en las ciencias sociales y resolver la aplicación del principio de promedios y de la variabilidad a los fenómenos sociales. Quételect fue el primero en realizar la aplicación práctica de todo el método Estadístico, entonces conocido, a las diversas ramas de la ciencia.Entretanto, en el período del 1800 al 1820 se desarrollaron dos conceptos matemáticos fundamentales para la teoría Estadística; la teoría de los errores de observación, aportada por Laplace y Gauss; y la teoría de los mínimos cuadrados desarrollada por Laplace, Gauss y Legendre. A finales del siglo XIX, Sir Francis Gaston ideó el método conocido por Correlación, que tenía por objeto medir la influencia relativa de los factores sobre las variables. De aquí partió el desarrollo del coeficiente de correlación creado por Karl Pearson y otros cultivadores de la ciencia biométrica como J. Pease Norton, R. H. Hooker y G. Udny Yule, que efectuaron amplios estudios sobre la medida de las relaciones.Los progresos más recientes en el campo de la Estadística se refieren al ulterior desarrollo del cálculo de probabilidades, particularmente en la rama denominada indeterminismo o relatividad, se ha demostrado que el determinismo fue reconocido en la Física como resultado de las investigaciones atómicas y que este principio se juzga aplicable tanto a las ciencias sociales como a las físicas.
1.Leer el texto "historia de la estadística"
2. Realizar un resúmen del anterior texto.
3. Graficar un pentágono, hexágono, heptágono, octágono, eneágono y decágono, señalando en cada uno de ellos los elementos de un polígono.
VER EL SIGUIENTE VIDEO.
ver este video.
Definición de Estadística
La Estadística trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones.
Un estudio estadístico consta de las siguientes fases:
Recogida de datos.
Organización y representación de datos.
Análisis de datos.
Obtención de conclusiones.
Conceptos de Estadística
Población
Una población es el conjunto de todos los elementos a los que se somete a un estudio estadístico.
Individuo
Un individuo o unidad estadística es cada uno de los elementos que componen la población.
Muestra
Una muestra es un conjunto representativo de la población de referencia, el número de individuos de una muestra es menor que el de la población.
Muestreo
El muestreo es la reunión de datos que se desea estudiar, obtenidos de una proporción reducida y representativa de la población.
Valor
Un valor es cada uno de los distintos resultados que se pueden obtener en un estudio estadístico. Si lanzamos una moneda al aire 5 veces obtenemos dos valores: cara y cruz.
Dato
Un dato es cada uno de los valores que se ha obtenido al realizar un estudio estadístico. Si lanzamos una moneda al aire 5 veces obtenemos 5 datos: cara, cara, cruz, cruz.
Variable estadística
Definición de variable
Una variable estadística es cada una de las características o cualidades que poseen los individuos de una población.
Tipos de variable estadísticas
Variable cualitativa
Las variables cualitativas se refieren a características o cualidades que no pueden ser medidas con números. Podemos distinguir dos tipos:
Variable cualitativa nominal
Una variable cualitativa nominal presenta modalidades no numéricas que no admiten un criterio de orden. Por ejemplo:
El estado civil, con las siguientes modalidades: soltero, casado, separado, divorciado y viudo.
Variable cualitativa ordinal o variable cuasicuantitativa
Una variable cualitativa ordinal presenta modalidades no númericas, en las que existe un orden. Por ejemplo:
La nota en un examen: suspenso, aprobado, notable, sobresaliente.
Puesto conseguido en una prueba deportiva: 1º, 2º, 3º, ...
Medallas de una prueba deportiva: oro, plata, bronce.
Variable cuantitativa
Una variable cuantitativa es la que se expresa mediante un número, por tanto se pueden realizar operaciones aritméticas con ella. Podemos distinguir dos tipos:
Variable discreta
Una variable discreta es aquella que toma valores aislados, es decir no admite valores intermedios entre dos valores específicos. Por ejemplo:
El número de hermanos de 5 amigos: 2, 1, 0, 1, 3.
Variable continua
Una variable continua es aquella que puede tomar valores comprendidos entre dos números. Por ejemplo:
La altura de los 5 amigos: 1.73, 1.82, 1.77, 1.69, 1.75.
En la práctica medimos la altura con dos decimales, pero también se podría dar con tres decimales.
Fracciones propias
Las fracciones propias son aquellas cuyo numerador es menor que el denominador. Su valor está comprendido entre cero y uno.
Ejemplo:
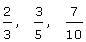
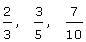
Fracciones impropias
Las fracciones impropias son aquellas cuyo numerador es mayor que el denominador. Su valor es mayor que 1.
Ejemplo:
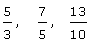
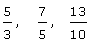
Número mixto
El número mixto o fracción mixta está compuesto de una parte entera y otra fraccionaria.
Para pasar de número mixto a fracción impropia:
1 Se deja el mismo denominador
2 El numerador se obtiene de la suma del producto del entero por el denominador más el numerador, del número mixto.
Ejemplo:
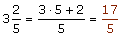
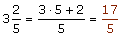
Para pasar una fracción impropia a número mixto:
1 Se divide el numerador por el denominador.
2 El cociente es el entero del número mixto.
3 El resto es el numerador de la fracción.
4 El denominador es el mismo que el de la fracción impropia.
Ejemplo:


Fracciones decimales
Las fracciones decimales tienen como denominador una potencia de 10.
Ejemplo:
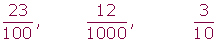
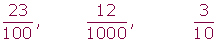
Fracciones equivalentes
Dos fracciones son equivalentes cuando el producto de extremos es igual al producto de medios.

a y d son los extremos
b y c son los medios
Ejemplo:
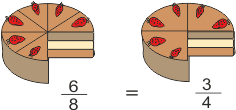

Calcula si son equivalentes las fracciones 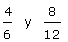 :
:
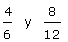 :
:
4 · 12 = 6 · 8  48 = 48 SÍ
48 = 48 SÍ
 48 = 48 SÍ
48 = 48 SÍ
2/3 - 4/12
Si se multiplica o divide el numerador y denominador de una fracción por un número entero, distinto de cero, se obtiene otra fracción equivalente a la dada.
Al primer caso le llamamos ampliar o amplificar.
Ejemplo:
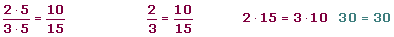
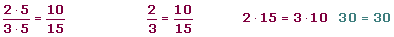
Simplificar fracciones
Simplificar una fracción es transformarla en una fracción equivalente más simple.
1 Para simplificar una fracción dividimos numerador y denominador por un mismo número.
2 Empezaremos a simplificar probando por los primeros números primos: 2, 3, 5, 7, ... Es decir, probamos a dividir numerador y denominador entre 2 mientras se pueda, después pasamos al 3 y así sucesivamente.
3 Se repite el proceso hasta que no haya más divisores comunes.
4 Si los términos de la fracción terminan en ceros, empezaremos quitando los ceros comunes finales del numerador y denominador, ¥ lo cual es equivalente a dividir numerador y denominador por la misma potencia de 10.
5 Si el número por el que dividimos es el máximo común divisor del numerador y denominador llegamos a una fracción irreducible.
Ejemplo:
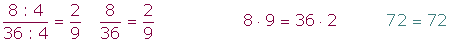
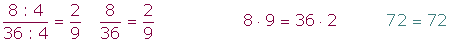
Fracciones irreducibles
Las fracciones irreducibles son aquellas que no se pueden simplificar, esto sucede cuando el numerador y el denominador son primos entre sí, ¥o lo que es lo mismo, cuando el mcd de ambos números es 1.
Ejemplo:
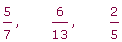
Suscribirse a:
Entradas (Atom)






